Question

Sketch the parabola y = f(x) which has the following properties:

1. f(-3) = 0
2. f(0) = 6
3. f(-1) = 0
4. f(x) > 0 when x < -1
5. f(x) < 0 when x > -1

Answer 1

Based on the given properties, we can sketch the parabola y = f(x) as follows:

1. The first property, f(-3) = 0, tells us that the parabola has an x-intercept at x = -3.

2. The second property, f(0) = 6, tells us that the parabola has a y-intercept at y = 6.

3. The third property, f(-1) = 0, tells us that the parabola has another x-intercept at x = -1.

4. The fourth and fifth properties tell us that the parabola is positive (above the x-axis) when x < -1 and negative (below the x-axis) when x > -1.

Based on these properties, we can sketch a parabola that opens downward with x-intercepts at x = -3 and x = -1 and a y-intercept at y = 6. The vertex of the parabola would be located at the midpoint of the two x-intercepts, which is (-3 + (-1)) / 2 = -2. Since the parabola opens downward and has a y-intercept of 6, the vertex must be located above the y-intercept.

Here is one possible sketch of the parabola y = f(x) based on the given properties:

Answer 2

See attachment.

Explanation:

The x-intercepts of a function are the points at which the curve crosses the x-axis, so when f(x) = 0.

Given f(-3) = 0 and f(-1) = 0, this indicates that the two x-intercepts of the parabola y = f(x) are x = -3 and x = -1.

For a parabola that opens upwards:

• f(x) > 0 for the x-values either side of the the x-intercepts.
• f(x) < 0 for the x-values between the the x-intercepts.

For a parabola that opens downwards:

• f(x) < 0 for the x-values either side of the the x-intercepts.
• f(x) > 0 for the x-values between the the x-intercepts.

The x-intercepts are x = -1 and x = -3.

Given that f(x) > 0 when x < -1, and f(x) < 0 when x > -1, this indicated that the parabola opens upwards.

The y-intercept is the point at which the curve crosses the y-axis, so when x = 0. Given f(0) = 6, this indicates that the y-intercept is y = 6.

The x-value of the vertex is the midpoint of the two x-intercepts.

Given the x-intercepts are x = -3 and x = -1, then the x-value of the vertex of the parabola is x = -2.

To find the y-value of the vertex, we need to create the equation of the function and substitute x = -2 into it.

Substitute the x-values into the intercept formula:

`\boxed{\begin{minipage}{6 cm}\underline{Intercept form of a quadratic equation}\\\\$y=a(x-p)(x-q)$\\\\where:\\ \phantom{ww}$\bullet$ $p$ and $q$ are the $x$-intercepts. \\ \phantom{ww}$\bullet$ $a$ is the leading coefficient.\\\end{minipage}}`

`y=a(x-(-3))(x-(-1))`

`y=a(x+3)(x+1)`

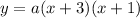
To find the value of a, we can substitute the given point (0, 6) into the equation:

`6=a(0+3)(0+1)`

`6=a(3)(1)`

`6=3a`

`a=2`

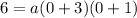
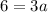
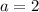
Substitute the found value of a into the equation and expand to standard form:

`y=2(x+3)(x+1)`

`y=2(x^2+4x+3)`

`y=2x^2+8x+6`

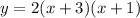
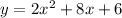
To find the y-value of the vertex, substitute x = -2 into the equation of the parabola:

`y=2(-2)^2+8(-2)+6=-2`

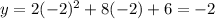
Therefore, the vertex of the parabola is (-2, -2).

Sketch an upwards opening parabola with:

• x-intercepts at x = -3 and x = -1.
• Vertex at (-2, -2).
• y-intercept at y = 6.

The x-value of the vertex is the axis of symmetry. Therefore, ensure your parabola has symmetry about the vertical line x = -2.

`\hrulefill`

Please note that there is likely an error in the properties you have been given. If the y-intercept is positive, and both x-intercepts are negative, the parabola opens upwards. Therefore, f(x) > 0 when x > -1, and f(x) < 0 when x < -1.