Question

Please help! maths functions

Answer 1

`\textsf{1)} \quad f(x)=-(1)/(4)(x-2)^2+(1)/(2)`

`\textsf{2)} \quad g(x)=-(1)/(4)(x+2)^2+(1)/(2)`

`\textsf{3)} \quad h(x)=(1)/(4)(x-2)^2-(1)/(2)`

`\textsf{4)} \quad p(x)=(1)/(4)(x+2)^2-(1)/(2)`

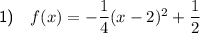
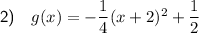
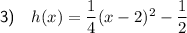
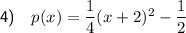
Explanation:

From inspection of the given graph, function f(x) is a parabola that opens downwards. Its vertex is (2, 1/2) and its y-intercept is (0, -1/2).

To determine the equation of f(x), we can use the vertex formula:

`\boxed{\begin{minipage}{5.6 cm}\underline{Vertex form of a quadratic equation}\\\\$y=a(x-h)^2+k$\\\\where:\\ \phantom{ww}$\bullet$ $(h,k)$ is the vertex. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}`

Substitute the vertex (2, 1/2) and the y-intercept (0, -1/2) into the formula to determine the value of a:

`\begin{aligned}y&=a(x-h)^2+k\\\\\implies -(1)/(2)&=a(0-2)^2+(1)/(2)\\\\-1&=4a\\\\a&=-(1)/(4)\end{aligned}`

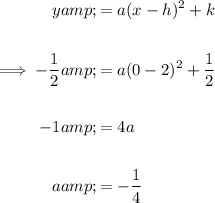
Substitute the found value of a and the vertex into the formula to create an equation for f(x):

`f(x)=-(1)/(4)(x-2)^2+(1)/(2)`

`\hrulefill`

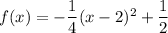
To reflect a function in the y-axis, negate the x-value of each point, but leave the y-value the same:

• Reflection in the y-axis: (x, y) → (-x, y)

Therefore, if g(x) is f(x) reflected in the y-axis, replace x with -x:

`\begin{aligned}g(x)&=f(-x)\\\\&=-(1)/(4)(-x-2)^2+(1)/(2)\\\\&=-(1)/(4)(x+2)^2+(1)/(2)\end{aligned}`

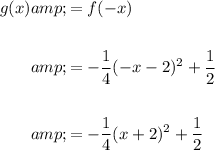
The vertex of g(x) is (-2, 1/2) and its y-intercept is (0, -1/2).

`\hrulefill`

To reflect a function in the x-axis, negate the y-value of each point, but leave the x-value the same:

• Reflection in the x-axis: (x, y) → (x, -y)

Therefore, if h(x) is f(x) reflected in the x-axis, then:

`\begin{aligned}h(x)&=-f(x)\\\\&=-\left(-(1)/(4)(x-2)^2+(1)/(2)\right)\\\\&=(1)/(4)(x-2)^2-(1)/(2)\end{aligned}`

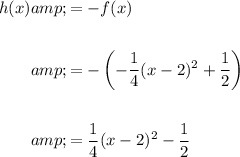
The leading coefficient is positive, so the parabola opens upwards.

The vertex of h(x) is (2, -1/2) and its y-intercept is (0, 1/2).

`\hrulefill`

If p(x) is g(x) reflected in the y-axis, then:

`\begin{aligned}p(x)&=-g(x)\\\\&=-\left(-(1)/(4)(-x-2)^2+(1)/(2)\right)\\\\&=(1)/(4)(-x-2)^2-(1)/(2)\\\\&=(1)/(4)(x+2)^2-(1)/(2)\end{aligned}`

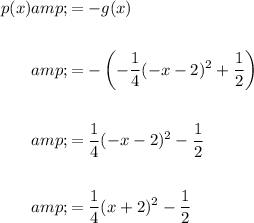
The leading coefficient is positive, so the parabola opens upwards.

The vertex of p(x) is (-2, -1/2) and its y-intercept is (0, 1/2).