Answer:
The spring would compress by approximately
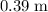 .
.
The elastic potential energy stored in the spring would be approximately
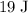 .
.
(Assuming that
 .)
.)
Step-by-step explanation:
Assuming that
 , the weight of this block (
, the weight of this block (
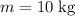 ) would be:
) would be:
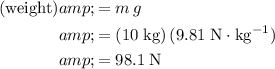 .
.
The spring compresses under the weight of this block. Dividing the external force
 by the spring constant
by the spring constant
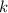 would give the displacement
would give the displacement
 from equilibrium:
from equilibrium:
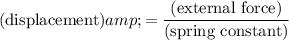 .
.
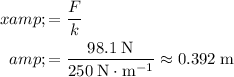 .
.
When a spring of spring constant
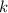 is compressed by a displacement of
is compressed by a displacement of
 , the elastic potential energy
, the elastic potential energy
 stored in this spring would be:
stored in this spring would be:
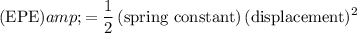 .
.
For the spring in this question:
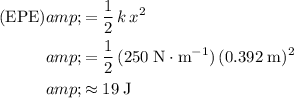 .
.