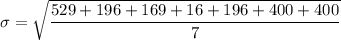 The formula for calculating standard deviation is
The formula for calculating standard deviation is
 , where
, where
 is the population standard deviation,
is the population standard deviation,
 is the population size,
is the population size,
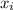 is each value from the population, and
is each value from the population, and
 is the population mean. We can substitute each value into the formula and simplify, which gives us our standard deviation.
is the population mean. We can substitute each value into the formula and simplify, which gives us our standard deviation.


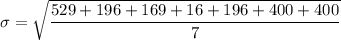
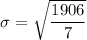
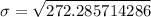
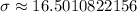
Our answer is
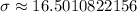 , or, for convenience,
, or, for convenience,
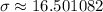 , which is the most digits you'll probably need for any calculations you make.
, which is the most digits you'll probably need for any calculations you make.
Hope this helps!