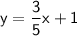Answer:
Option D
Explanation:
Slope intercept form:
(-5, -2) ; x₁ = -5 & y₁ = -2
(5 , 4) ; x₂ = 5 & y₂ = 4
Plugin the points in the below mentioned formula and find the slope.
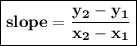
![\sf = (4-[-2])/(5-[-5])\\\\\\=(4+2)/(5+5)\\\\=(6)/(10)\\\\=(3)/(5)](https://img.qammunity.org/2024/formulas/mathematics/college/yssym1pkuch9fnnrb3forbgw9au2pkbl5e.png)
Equation of slope-intercept form: y =mx + b
Here, m is the slope and b is the y-intercept.

The line is passing through (5, 4). So, substitute the points in the equation and find the y-intercept.
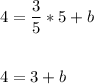
4 - 3 = b
b = 1
Slope intercept form of the equation: