Question

Newton's law of universal gravitation states that the gravitational force exened by an object on any other object anywhere in the universe by Gmm F= where G is the universal gravitational constant (6.67 x 10-11 N.m 2kg 2), ms is mass 1, m2 is mass 2, and r is the distance between the two masses (from conter to contor). If the distance between the two masses doubles, the gravitational force between the two masse O remains the same O is reduced to 1/4. O is reduced to 1/9, O doubles O quadruples.

Answer 1

Gravitational force between the two will reduce to
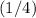`(1/4)` the original value.

Step-by-step explanation:

The distance between the two objects was originally
`r`. The gravitational force between the two objects would be:

`\displaystyle F = (G\, m_(1)\, m_(2))/(r^(2))`.

If the distance between the two is doubled, the new distance will become
`2\, r`. The new gravitational force between the two will become:

`\begin{aligned}(G\, m_(1)\, m_(2))/((2\, r)^(2)) &= (G\, m_(1)\, m_(2))/(4\, r^(2)) = (1)/(4)\, \left((G\, m_(1)\, m_(2))/(r^(2))\right)\end{aligned}`.

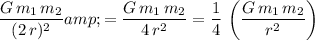In other words, the force between the two objects will become one-quarter of the initial value.