The equation is :
↬ y = x + 1
Solution:
We Know
If two lines are parallel to each other, then their slopes are equal. The slope of y = x - 1 is 1. Hence, the slope of the line that is parallel to that line is 1.
We shouldn't forget about a point on the line : (-3, -2).
I plug that into a point-slope which is :
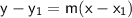
Slope is 1 so

Simplify
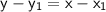
Now I plug in the other numbers.
-3 and -2 are x and y, respectively.
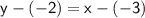
Simplify

We're almost there, the objective is to have an equation in y = mx + b form.
So now I subtract 2 from each side
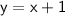
Hence, the equation is y = x + 1