Answer:
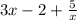
Explanation:
To divide the polynomial (9x^3 - 6x^2 + 15x) by the monomial 3x^2, we can write it as:
(9x^3 - 6x^2 + 15x) ÷ (3x^2)
To simplify the division, we divide each term of the polynomial by 3x^2:
(9x^3 ÷ 3x^2) - (6x^2 ÷ 3x^2) + (15x ÷ 3x^2)
To divide monomials with the same base, we subtract the exponents. So:
9x^3 ÷ 3x^2 = 9/3 * (x^3/x^2) = 3x^(3-2) = 3x
(-6x^2) ÷ (3x^2) = -6/3 * (x^2/x^2) = -2
15x ÷ 3x^2 = 15/3 * (x/x^2) = 5/x
Putting it all together, we have:
(9x^3 - 6x^2 + 15x) ÷ (3x^2) = 3x - 2 + 5/x
Therefore, the division of (9x^3 - 6x^2 + 15x) by 3x^2 is 3x - 2 + 5/x.