Answer:
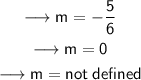
In-depth explanation:
Hi there, let's find the slope.
Main Idea: To find the slope, use the formula:

Where:

Question 1
Find the slope of the line passing through the points (-2, 3) and (-8, 8)
Plug the data into the formula:


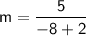
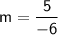

Therefore, the slope of the line that passes through the points (-2,3) and (-8,8) is -5/6.

Question 2
Find the slope of the line passing through the points (-7, 6) and (3,6)
Plug the data into the formula:
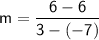
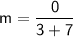

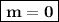
Therefore, the slope of the line passing through the points (-7,6) and (-3,6) is 0.

Question 3
Find the slope of the line passing through the points (-2,9) and (-2,5).
Plug the data into the formula:
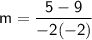
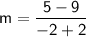
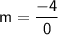
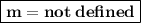
Therefore, the slope of the line that passes through (-2,9) and (-2,5) is not defined.