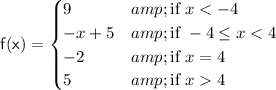
To sketch the graph of this function, we plot the points and lines as follows:

1.
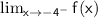 : The limit as x approaches -4 from the left side. Since the function is continuous at -4, the limit exists and is equal to the value of the function at that point. So,
: The limit as x approaches -4 from the left side. Since the function is continuous at -4, the limit exists and is equal to the value of the function at that point. So,
 .
.
2.
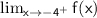 : The limit as x approaches -4 from the right side. Again, since the function is continuous at -4 , the limit exists and is equal to the value of the function at that point. So,
: The limit as x approaches -4 from the right side. Again, since the function is continuous at -4 , the limit exists and is equal to the value of the function at that point. So,
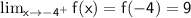 .
.
3.
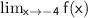 : The limit as x approaches -4. Since the left and right limits both exist and are equal, the overall limit exists and is equal to the common value. So,
: The limit as x approaches -4. Since the left and right limits both exist and are equal, the overall limit exists and is equal to the common value. So,
 .
.
4.
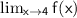 : The limit as x approaches 4. Since the function has a discontinuity at
: The limit as x approaches 4. Since the function has a discontinuity at
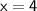 (a jump from
(a jump from
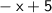 to (-2), the limit does not exist. So,
to (-2), the limit does not exist. So,
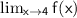 is DNE.
is DNE.
5.
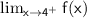 : The limit as x approaches 4 from the right side. Since the function is continuous at 4, the limit exists and is equal to the value of the function at that point. So,
: The limit as x approaches 4 from the right side. Since the function is continuous at 4, the limit exists and is equal to the value of the function at that point. So,
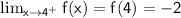 .
.
6.
 : The limit as x approaches 4 from the right side, multiplied by
: The limit as x approaches 4 from the right side, multiplied by
 . Since the function is continuous at 4, we can evaluate this limit by substituting
. Since the function is continuous at 4, we can evaluate this limit by substituting
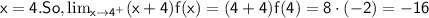 .
.
That's it!