Given inequality:

To find the limit as x approaches 1 of f(x), we can use the Squeeze Theorem. Since
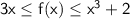 holds for
holds for
 , we can evaluate the limits of the lower and upper bounds and check if they are equal at x = 1.
, we can evaluate the limits of the lower and upper bounds and check if they are equal at x = 1.
1. Lower bound: 3x
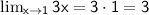
2. Upper bound:
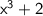

Since the limits of both the lower and upper bounds are equal to 3 at x = 1, we can conclude that:

That's it!