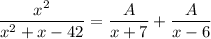Question

MY NOT .. DETAILS SCALCET9M 7.4.005. Write out the form of the partial fraction decomposition of the function (as in this example). Do not determine the numerical values of the coefficients. (a) x5 + 36 (x2 - x)(x4 + 12x2 + 36) (b) x2 x² + x - 42

Answer 1

The partial fraction decomposition of the functions are
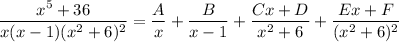`(x^5 + 36)/(x(x - 1)(x^2 + 6)^2) = (A)/(x) +(B)/(x - 1) + (Cx + D)/(x^2 + 6) + (Ex + F)/((x^2 + 6)^2)` and
`(x^2)/(x^2 + x - 42) = (A)/(x + 7) + (A)/(x - 6)`

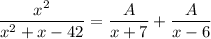
Writing out the form of the partial fraction decomposition of the function

From the question, we have the following parameters that can be used in our computation:

`(x^5 + 36)/((x^2 - x)(x^4 + 12x^2 + 36))`

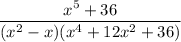
Expand and factorize

So, we have

`(x^5 + 36)/(x(x - 1)(x^2 + 6)^2)`

In the denominator, we have that (x² + 6) is repeated

So, it will also be repeated when decomposed into partial fractions

So, we have

`(x^5 + 36)/(x(x - 1)(x^2 + 6)^2) = (A)/(x) +(B)/(x - 1) + (Cx + D)/(x^2 + 6) + (Ex + F)/((x^2 + 6)^2)`

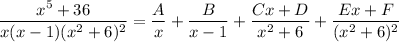
This means that

`(x^5 + 36)/(x(x - 1)(x^2 + 6)^2) = (A)/(x) +(B)/(x - 1) + (Cx + D)/(x^2 + 6) + (Ex + F)/((x^2 + 6)^2)`

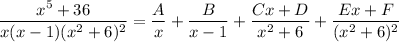
Next, we have

`(x^2)/(x^2 + x - 42)`

Expand and factorize

So, we have

`(x^2)/((x + 7)(x - 6))`

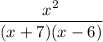
The denominators are linear factors

So, we have

`(x^2)/((x + 7)(x - 6)) = (A)/(x + 7) + (A)/(x - 6)`

This means that

`(x^2)/(x^2 + x - 42) = (A)/(x + 7) + (A)/(x - 6)`

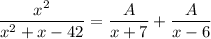
Hence, the partial fraction decomposition of the functions are
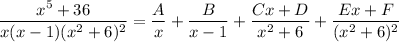`(x^5 + 36)/(x(x - 1)(x^2 + 6)^2) = (A)/(x) +(B)/(x - 1) + (Cx + D)/(x^2 + 6) + (Ex + F)/((x^2 + 6)^2)` and
`(x^2)/(x^2 + x - 42) = (A)/(x + 7) + (A)/(x - 6)`