Question

Equilateriall triangle. Find the length of side X in simple radical form with a rational denominator

Answer 1

x = 4

Explanation:

since the triangle is equilateral then the vertex angles are congruent, each 60°

using the sine ratio in the right triangle with x as its hypotenuse and the exact value

sin60° =
`(√(3) )/(2)` , then

sin60° =
`(opposite)/(hypotenuse)` =
`(√(12) )/(x)` =
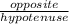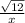`(√(3) )/(2)` ( cross- multiply )

x ×
`√(3)` = 2
`√(12)` ( divide both sides by
`√(3)` )

x =
`(2√(12) )/(√(3) )` = 2 ×
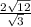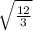`\sqrt{(12)/(3) }` = 2 ×
`√(4)` = 2 × 2 = 4