Question

NO LINKS!! URGENT HELP PLEASE!!

What is the surface of this problem? Please show work!!​

Answer 1

720 m^2

Explanation:

Solution:

The formula for the surface area of a triangular prism is:

Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)

= (S1 +S2 + S3)L + bh

where,

• b is the bottom edge of the base triangle,
• h is the height of the base triangle,
• L is the length of the prism and
• S1, S2, and S3 are the three edges (sides) of the base triangle
• (bh) is the combined area of the two triangular faces [2 × (1/2 × bh)] = bh

Given:

side 1 (S1) : 5 m

side 2(S2): x m

side 3(S3): 12 m

length (l)=22m

Here we need to find side 2, we can easily find it using Pythagoras' theorem.

a^2+b^2=c^2

5^2+12^2=x^2

x^2=169

x=
`√(169)=13 m`

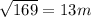
therefore, side 2 is 13 m.

Substituting value in the formula

Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)

= (S1 +S2 + S3)L + bh

Surface Area=(5+13+12)*22+5*12= 720 m^2

Answer 2

720 m²

Explanation:

The given diagram shows a triangular prism.

A triangular prism consists of two congruent triangular bases and three rectangular faces connecting these bases.

To calculate the surface area of the triangular prism, we first need to calculate the length of the hypotenuse of the right triangular base. To do this, we can use Pythagoras Theorem:

`\begin{aligned}\sf Hypotenuse\;of\;triangular\;base&=√(5^2+12^2)\\&=√(25+144)\\&=√(169)\\&=13\; \sf m\end{aligned}`

The surface area of a triangular prism is the sum of the areas of all its faces. Therefore:

`\begin{aligned}\sf Total\;surface\;area&=2\left((1)/(2) \cdot 5 \cdot 12\right)+12\cdot 22+5 \cdot 22+13 \cdot 22\\\\&=60+264+110+286\\\\&=720\; \sf m^2\end{aligned}`

Therefore, the total surface area of the given triangular prism is 720 m².