Question

Find the relative maximum and minimum values of f(x,y) = 6x3 - y2 + 6xy + 2.

Answer 1

(0,0) is a saddle point

(-1,-3) is a local maximum

Explanation:

Find critical points

`f(x,y)=6x^3-y^2+6xy+2\\\\(\partial f)/(\partial x)=18x^2+6y\rightarrow18x^2+6y=0\\\\(\partial f)/(\partial y)=-2y+6x\rightarrow6x-2y=0`

`6x-2y=0\\3x=y`

`18x^2+6y=0\\18x^2+6(3x)=0\\18x^2+18x=0\\x^2+x=0\\x(x+1)=0\\x=0,-1`

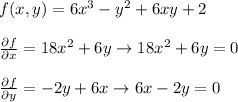
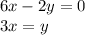
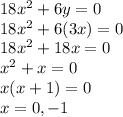
Therefore, the critical points are
`(0,0)` and
`(-1,-3)`.

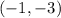Determine value of Hessian Matrix at critical points

`H=\bigr((\partial^2 f)/(\partial x^2)\bigr)\bigr((\partial^2 f)/(\partial y^2)\bigr)-\bigr((\partial^2 f)/(\partial x \partial y)\bigr)^2\\\\H=(36x)(-2)-6^2\\\\H=-72x-36`

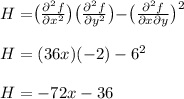
For (0,0):

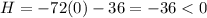`H=-72(0)-36=-36 < 0`, so (0,0) is a saddle point

For (-1,-3):

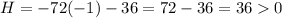`H=-72(-1)-36=72-36=36 > 0`, so (-1,-3) is either a local maximum or minimum. Since
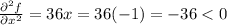`(\partial^2 f)/(\partial x^2)=36x=36(-1)=-36 < 0`, then (-1,-3) is a local maximum.