Question

How to solve x2 -6x -20 =7

Answer 1

-6.75

Explanation:

To find x, first you factorize the two coefficients of the variable 2x and -6x since x2=2x.

x(2-6)-20=7

x(-4)-20=7

x(-4)=27

x=27/-4

x=-6.75

Answer 2

Hello !

Answer:

`\large \boxed{\sf x=9 \ \ \ or \ \ \ x=-3 }`

Explanation:

We are looking for the value of x that satifies the following equation :

`\sf x^2 -6x -20 =7`

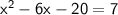
Le'ts substract 7 from both sides :

`\sf x^2 -6x -27 =0`

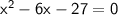
This equation is a quadratic equation in the form ax²+bx+c=0

The solution of this equation is given by the quadratic formula :

`\sf x=(-b\pm√(\Delta))/(2a)`

Where
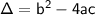`\sf \Delta = b^2-4ac` is the discriminant.

There are 3 cases depending on the values of the discriminant :

• 
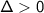  `\sf \Delta > 0` : 2 real roots
• 
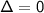  `\sf \Delta = 0` : 1 real roots
• 
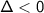  `\sf \Delta < 0` : no real root

Let's calculate the discriminant :

`\sf \Delta = (-6)^2-4*1*(-27)\\\Delta = 36+108\\\underline{\sf \Delta = 144 > 0}`

There are 2 real roots.

Now let's use the quadratic formula to find the two roots.

`\sf x=(-(-6)\pm √(144))/(2*1) \\x=(6\pm12)/(2) \\\boxed{\sf x=9 \ \ \ or \ \ \ x=-3 }`

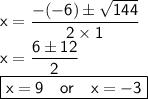
Have a nice day ;)