Question

NO LINKS!! URGENT HELP PLEASE!!!

Solve each continuous exponential growth problem.

24. A savings account balance is compounded continuously. If the interest rate is 3% per year and the current balance is $1727.00, what will the balance be 6 years from now?

Answer 1

$2,067.59

Explanation:

To calculate the balance of the savings account, we can use the continuous compounding interest formula:

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

Given values:

• P = $1,727.00
• r = 3% = 0.03
• t = 6 years

Substitute the given values into the formula and solve for A:

`\begin{aligned}A&=1727 \cdot e^(0.03 \cdot 6)\\&=1727 \cdot e^(0.18)\\&=1727 \cdot 1.19721736...\\&=2067.59438...\\&=2067.59\end{aligned}`

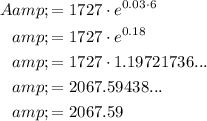
Therefore, the balance of the savings account 6 years from now is $2,067.59.