Question

NO LINKS!! URGENT HELP PLEASE!!

Solve each problem involving direct or inverse variation.

26. If y varies directly as x, and y = 15/4 when x = 15, find y when x = 11

27. If y varies inversely as x, and y = 4 when x = 9, find when x = 7

Answer 1

26) y = 11/4

27) y = 36/7

Explanation:

Question 26

Direct variation is a mathematical relationship between two variables where a change in one variable directly corresponds to a change in the other variable. It is represented by the equation y = kx, where y and x are the variables and k is the constant of variation.

To find the constant of variation, k, substitute the given values of y = 15/4 when x = 15 into the direct variation equation and solve for k:

`\begin{aligned}y&=kx\\\\(15)/(4)&=15k\\\\k&=(1)/(4)\end{aligned}`

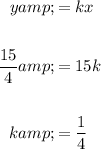
To find the value of y when x = 11, substitute the found value of k and x = 11 into the direct variation equation, and solve for y:

`\begin{aligned}y&=kx\\\\y&=(1)/(4) \cdot 11\\\\y&=(11)/(4)\end{aligned}`

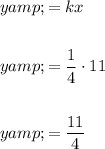
Therefore, if y varies directly as x, then y = 11/4 when x = 11.

`\hrulefill`

Inverse variation is a mathematical relationship between two variables where an increase in one variable results in a corresponding decrease in the other variable, and vice versa, while their product remains constant. It is represented by the equation y = k/x, where y and x are the variables and k is the constant of variation.

To find the constant of variation, k, substitute the given values of y = 4 when x = 9 into the inverse variation equation and solve for k:

`\begin{aligned}y&=(k)/(x)\\\\4&=(k)/(9)\\\\k&=36\end{aligned}`

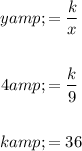
To find the value of y when x = 7, substitute the found value of k and x = 7 into the inverse variation equation, and solve for y:

`\begin{aligned}y&=(k)/(x)\\\\y&=(36)/(7)\end{aligned}`

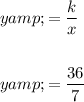
Therefore, if y varies inversely as x, then y = 36/7 when x = 7.

Answer 2

see explanation

Explanation:

26

given y varies directly as x then the equation relating them is

y = kx ← k is the constant of variation

to find k use the condition y =
`(15)/(4)` when x = 15

`(15)/(4)` = 15k ( divide both sides by 15 )

`((15)/(4) )/(15)` = k , then

k =
`(15)/(4)` ×
`(1)/(15)` =
`(1)/(4)`

y =
`(1)/(4)` x ← equation of variation

when x = 11 , then

y =
`(1)/(4)` × 11 =
`(11)/(4)`

27

given y varies inversely as x then the equation relating them is

y =
`(k)/(x)` ← k is the constant of variation

to find k use the condition y = 4 when x = 9

4 =
`(k)/(9)` ( multiply both sides by 9 )

36 = k

y =
`(36)/(x)` ← equation of variation

when x = 7 , then

y =
`(36)/(7)`