Question

NO LINKS!! URGENT HELP PLEASE!!!

Determine if the sequence is arithmetic. If it is, find the common difference, the 52nd term, and the explicit formula.

34. -11, -7, -3, 1, . . .

Given the explicit formula for an arithmetic sequence find the common difference and the 52nd term.

35. a_n = -30 - 4n

Answer 1

`\begin{aligned}\textsf{34)} \quad d&=4\\a_n&=4n-15\\a_(52)&=193\end{aligned}`

`\begin{aligned}\textsf{35)} \quad d&=-4\\a_(52)&=-238\end{aligned}`

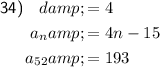
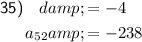
Explanation:

Question 34

An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant.

Given sequence:

• -11, -7, -3, 1, ...

To determine if the given sequence is arithmetic, calculate the differences between consecutive terms.

`a_4-a_3=1-(-3)=4`

`a_3-a_2=-3-(-7)=4`

`a_2-a_1=-7-(-11)=4`

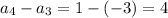
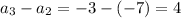
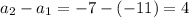
As the differences are constant, the sequence is arithmetic, with common difference, d = 4.

The explicit formula for an arithmetic sequence is:

`\boxed{a_n=a+(n-1)d}`

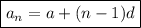
where:

• a is the first term of the sequence.
• n is the position of the term
• d is the common difference between consecutive terms.

To find the explicit formula for the given sequence, substitute a = -11 and d = 4 into the formula:

`\begin{aligned}a_n&=-11+(n-1)4\\&=-11+4n-4\\&=4n-15\end{aligned}`

To find the 52nd term, simply substitute n = 52 into the formula:

`\begin{aligned}a_(52)&=4(52)-15\\&=208-15\\&=193\end{aligned}`

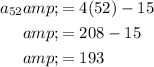
Therefore, the 52nd term is a₅₂ = 193.

`\hrulefill`

Question 35

Given explicit formula for an arithmetic sequence:

`a_n=-30-4n`

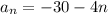
To find the common difference, we need to compare it with the explicit formula for the nth term:

`\begin{aligned}a_n&=a+(n-1)d\\&=a+dn-d\\&=a-d+dn\end{aligned}`

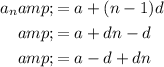
The coefficient of the n-term is -4, therefore, the common difference is d = -4.

To find the 52nd term, simply substitute n = 52 into the formula:

`\begin{aligned}a_(52)&=-30-4(52)\\&=-30-208\\&=-238\end{aligned}`

Therefore, the 52nd term is a₅₂ = -238.

Answer 2

• #34. aₙ = 4n - 15; a₅₂ = 193

• #35. a₅₂ = -238; d = - 4

-----------------

Question 34

Find the differences in the sequence -11, -7, -3, 1, ...

• 1 - (-3) = 4,
• -3 - (-7) = 4,
• -7 - (-11) = 4

The difference is common, so the sequence is an AP.

The nth term is:

• 
  `a_n=a_1+(n-1)d`

• 
  `a_n=-11+(n-1)*4=-11+4n-4=4n-15`

Find the 52nd term:

• 
  `a_(52)=4*52-15=208-15=193`

Question 35

Find the 52nd term using the given formula:

• 
  `a_(52)=-30-4*52=-30-208=-238`

Find the previous term:

• 
  `a_(51)=-30-4*51=-30-204=-234`

Find the common difference:

• 
  `d=a_(52)-a_(51)=-238-(-234)=-4`