Answer:
see explanation
Explanation:
to find the first 5 terms substitute n = 1, 2, 3, 4, 5 into the explicit formula
36
a₁ = -
 = -
= -
 = - 1 [
= - 1 [
 = 1 ]
= 1 ]
a₂ = -
 = -
= -
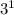 = - 3
= - 3
a₃ = -
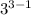 = - 3² = - 9
= - 3² = - 9
a₄ = -
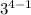 = - 3³ = - 27
= - 3³ = - 27
a₅ = -
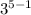 = -
= -
 = - 81
= - 81
the first 5 terms are - 1, - 3, - 9, - 27, - 81
to find a₈ substitute n = 8 into the explicit formula
a₈ = -
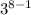 = -
= -
 = - 2187
= - 2187
37
to find the first 5 terms substitute n = 1, 2, 3, 4, 5 into the explicit formula
a₁ = 2 ×
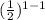 = 2 ×
= 2 ×
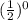 = 2 × 1 = 2
= 2 × 1 = 2
a₂ = 2 ×
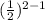 = 2 ×
= 2 ×
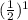 = 2 ×
= 2 ×
 = 1
= 1
a₃ = 2 ×
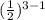 = 2 ×
= 2 ×
 = 2 ×
= 2 ×
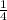 =
=

a₄ = 2 ×
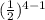 = 2 × (
= 2 × (
 )³ = 2 ×
)³ = 2 ×
 =
=
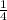
a₅ = 2 ×
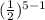 = 2 ×
= 2 ×
 = 2 ×
= 2 ×
 =
=

the first 5 terms are 2 , 1 ,
 ,
,
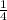 ,
,

to find a₈ substitute n = 8 into the explicit formula
a₈ = 2 ×
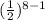 = 2 ×
= 2 ×
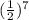 = 2 ×
= 2 ×
 =
=
