To find where the tangent line has the largest slope on the curve y = 1 + 40x³ − 3x⁵, we calculate the function's derivative, set it equal to zero to find the critical points, and then apply the second derivative test to determine maxima. The slope is largest at x = -√8 and x = √8.
To find the points on the curve where the tangent line has the largest slope at the smaller and larger x-values, we'll need to work with the first derivative of the function.
Given
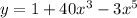 , the slope of the tangent line to a curve at any point is given by the derivative of y with respect to x,
, the slope of the tangent line to a curve at any point is given by the derivative of y with respect to x,
 .
.
Let's first find the derivative of y with respect to x:
![\[y = 1 + 40x^3 - 3x^5\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x45dvx2fz2m36cjldf5u2dbsru013l0354.png)
![\[(dy)/(dx) = (d)/(dx) (1) + (d)/(dx) (40x^3) - (d)/(dx) (3x^5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/abfp2pwe9txmqqa5mt3x7gphsc0prr6rvs.png)
![\[(dy)/(dx) = 0 + 120x^2 - 15x^4\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1iz5qw7z9x0o759bg5ltl8aqfxmrytkaf8.png)
To find the points where the tangent line has the largest slope, we'll need to find the critical points of the derivative, i.e., where \(dy/dx = 0\) or where the derivative is undefined.
![\[(dy)/(dx) = 120x^2 - 15x^4\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cw3bxmwg9z5r1hzt94vaan58wdarayy6gq.png)
Setting the derivative equal to zero to find critical points:
![\[120x^2 - 15x^4 = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qui4uf86z863yfox09yp2l3ulvzqeclsww.png)
![\[x^2(120 - 15x^2) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pvx64lcgzk9zchtz3rs6za7ct75cwmwawn.png)
This equation gives us two critical points:
1.
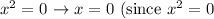 has a solution at
has a solution at

2.
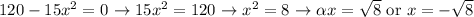
Now, to determine which critical point corresponds to the largest slope at smaller and larger x-values, we'll evaluate the second derivative or check the slopes at these points.
![\[(d^2y)/(dx^2) = (d)/(dx)(120x^2 - 15x^4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/e8u9j3nxdbov44wrc7hkx2ksx5l80tl7c0.png)
![\[(d^2y)/(dx^2) = 240x - 60x^3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1zbu7c4cvjdldayin3gtydtn29mw5bwybx.png)
Now, substitute the critical points (x = 0) and
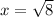 into the second derivative:
into the second derivative:
1. For (x = 0):
![\[d^2y/dx^2 = 240(0) - 60(0)^3 = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/99uv4puoj96n0h4z7oaeaj4ivz1ke64pte.png)
2. For \(x = \sqrt{8}\):
![\[d^2y/dx^2 = 240(√(8)) - 60(√(8))^3\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/36nkmx8e6856vdty925qo6ejofma4zg4r9.png)
![\[d^2y/dx^2 = 240√(8) - 60(8√(8))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k1hnwkwehm8dpi98u3s2rbyrrbt6vg42mw.png)
![\[d^2y/dx^2 = 240√(8) - 480√(8)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6ji6zvt964wg5lhon33gqucmhazzwon8vb.png)
![\[d^2y/dx^2 = -240√(8) < 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pg2x7wm7q7075tu54u3kc6azyhoegx5jzj.png)
From the second derivative test, the point
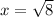 yields a negative second derivative, indicating a local maximum. Therefore, at
yields a negative second derivative, indicating a local maximum. Therefore, at
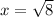 , the slope of the tangent line is largest among the critical points for the larger x-value.
, the slope of the tangent line is largest among the critical points for the larger x-value.
However, since
 correspond to the same absolute value of x but with opposite signs, for the smallest x-value, the slope will also be the largest at
correspond to the same absolute value of x but with opposite signs, for the smallest x-value, the slope will also be the largest at
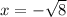 .
.