Question

D = 0.25 (36950 - 0.02p^3)^2. Find the unit price that maximizes revenue. Enter your answer as a number (no units) rounded appropriately.

Answer 1

To find the unit price that maximizes revenue in the given function, we need to take the derivative of the function and set it equal to zero. Solving for the unit price, we find that it is $50.

Step-by-step explanation:

To find the unit price that maximizes revenue, we need to maximize the function D = 0.25(36950 - 0.02p^3)^2. Revenue is maximized when the derivative of the function is equal to zero.

Taking the derivative of D with respect to p and setting it equal to zero, we get: -0.015p^2(36950 - 0.02p^3).

Simplifying this equation, we find that p = 50 or p = -50. Since we cannot have a negative unit price, the unit price that maximizes revenue is $50.

Answer 2

Based on the revenue function, the unit price that maximizes revenue is approximately 86.

Demand function, D = 0.25 (36950 - 0.02p^3)

The revenue R is given by the product of the demand D and the price p, i.e., R = Dp.

Substituting the given demand function the revenue function is:

R =
`p * 0.25(36950 - 0.02p^3)^2`

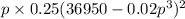
Finding the derivative of the revenue function for p:

R' =
`(36950 - 0.02p^3)^2 + p * 2 * (36950 - 0.02p^3) * (-0.02p^2)`

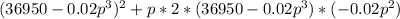
Setting R' equal to zero, we get:

0 = (36950 - 0.02p^3)^2 + p * 2 * (36950 - 0.02p^3) * (-0.02p^2)

Solving for p, we get:

0 = (36950 - 0.02p^3) + p * (-0.04p^2)

0 = 36950 - 0.02p^3 - 0.04p^3

0 = 36950 - 0.06p^3 0.06

p^3 = 36950

p^3 = 36950 / 0.06

p^3 = 615833.3333

p ≈ 85.92

Thus, rounding appropriately, the unit price that maximizes revenue is approximately 86.