Answer:
x = 12
Side length =
 in
in
Explanation:
Area of the given hexagon = 6 × (Area of the triangular section)
Area of the triangular section =
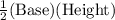
=
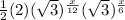
=
![(√(3))^{(x)/(12)}[(√(3))^2]^{(x)/(12)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/tv74qs0bida8glkppzxmx6rly997457pt1.png)
=

=

Now area of the given hexagon =
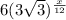
Since, area of the hexagon is =
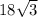 in²
in²
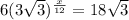
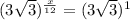

x = 12
Therefore, side length =

=
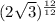
=
 in.
in.