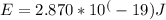Question

A mercury atom emits a photon when an electron in the atom moves from energy level f to energy level d. Determine the energy of the emitted photon, in joules.​

Answer 1

The energy of the emitted photon is approximately 2.870 x 10^(-19) joules.

Step-by-step explanation:

The energy of a photon can be calculated using the formula:

E = hc/λ

where E is the energy, h is Planck's constant, c is the speed of light
`(3.00 * 10^8 m/s)`, and λ is the wavelength.

In this case, the wavelength is given as 435.8 nm. To convert it to meters, we divide by 10^9:

`y = 435.8 nm = 435.8 x 10^(-9) m`

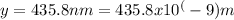
Plugging these values into the formula, we get:

`E = (6.626 x 10^(-34) Js) * (3.00 x 10^8 m/s) / (435.8 x 10^(-9) m)`

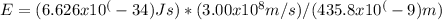
Simplifying the expression gives us the energy of the emitted photon:

`E = 2.870 * 10^(-19) J`

Answer 2

The energy of a photon emitted by an electron transition is given by the difference between the initial and final energy levels of the electron:

E = hf

where E is the energy of the photon, h is Planck's constant (6.626 x 10^-34 J s), and f is the frequency of the photon.

To determine the energy of the emitted photon in joules, we need to know the energy difference between the two energy levels of the electron. The energy levels of an electron in a mercury atom are quantized and can be calculated using the Rydberg equation:

1/λ = RZ^2(1/n1^2 - 1/n2^2)

where λ is the wavelength of the emitted photon, R is the Rydberg constant (1.097 x 10^7 m^-1), Z is the atomic number of mercury (80), and n1 and n2 are the initial and final energy levels, respectively.

Assuming n1 = f and n2 = d, we can rearrange the Rydberg equation to solve for the energy difference between the two energy levels:

ΔE = hc/λ = RZ^2hc(1/n2^2 - 1/n1^2)

where c is the speed of light (2.998 x 10^8 m/s).

Substituting the relevant values, we get:

ΔE = (6.626 x 10^-34 J s)(2.998 x 10^8 m/s)/(546.1 x 10^-9 m) = 4.535 x 10^-19 J

Therefore, the energy of the emitted photon is 4.535 x 10^-19 joules.