Question

A hockey puck is given an initial speed of 4.3 m/s.

Part A) If the coefficient of kinetic friction between the puck and the ice is 0.05, how far does the puck slide before coming to rest? Solve this problem using conservation of energy.

Answer 1

Using conservation of energy, the hockey puck with an initial velocity of 4.3 m/s and a coefficient of kinetic friction of 0.05 will slide 1.88 meters before coming to rest.

Step-by-step explanation:

To solve this problem, we will use the work-energy principle which is a part of conservation of energy. The work done by the friction force will equal the change in kinetic energy of the puck, therefore bringing it to rest.

The work done by friction (
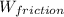`W_{friction`) is equal to the frictional force multiplied by the distance the puck slides (d). Since kinetic friction force is the product of the coefficient of kinetic friction (μ) and the normal force (N), and the normal force for a horizontal surface is mg where m is mass and g is acceleration due to gravity, we have:

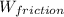`W_{friction`= frictional force × d = μmgd

The initial kinetic energy (
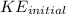`KE_{initial`) of the hockey puck is given by:

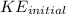`KE_{initial` = ½mv² where m is mass and v is the initial velocity.

Since the puck comes to rest, its final kinetic energy (
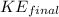`KE_{final`) is zero. Thus, the work done by friction is equal to the negative of the initial kinetic energy:

-½mv² = μmgd

After rearranging the equation to solve for d, we have:

d = -½v² / (μg)

Plugging in the known values, m = mass of puck, v = 4.3 m/s, μ = 0.05, and g = 9.8 m/s² we get:

d = -½(4.3 m/s)² / (0.05 × 9.8 m/s²)

d = 1.88 m

The hockey puck will slide 1.88 meters before coming to rest.