Question

Write an equation of the line perpendicular to line MN that goes through point Q.

Francisco has solved the problem for you, but made a mistake.

Find the error in the work and correct the mistake. Show your work for full credit.

Francisco’s work:
Step 1: Slope of MN: 1/4

Step 2: Slope of the line perpendicular: 4

Step 3: y - y = m(x - x) Q(6, -2)
y - (- 2) = 4 (x - 6)

Step 4: y + 2 = 4x - 24

Step 5: y + 2 - 2 = 4x - 24 - 2

Step 6: y = 4x - 26

Step completed incorrectly: ___
(I believe the step completed incorrectly is 2? But I’m not very sure on the showing my work part as well.)

Answer 1

Step completed incorrectly: 2

Correct Answer: y = -4x + 22

Explanation:

The graph is a straight line through points M(4, -1) and N(8, 0). Point Q is located at (6, -2).

To calculate the slope of the line, substitute the points into the slope formula:

`\textsf{Slope $(m)$}=(y_2-y_1)/(x_2-x_1)=(0-(-1))/(8-4)=(1)/(4)`

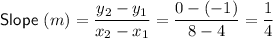
Therefore, the slope of MN is 1/4, so step 1 of Francisco's calculations is correct.

If two lines are perpendicular to each other, the slopes of these lines are negative reciprocals. The negative reciprocal of a number is its negative inverse.

The negative reciprocal of 1/4 is -4.

Therefore, the slope of the perpendicular line is -4.

So Francisco has made an error in his calculation in step 2 by not making the perpendicular slope negative.

Corrected work

`\textsf{Step 1:} \quad \sf slope\;of\;MN:\; (1)/(4)`

`\textsf{Step 2:} \quad \sf slope\;of\;the\;line\;perpendicular:\; -4`

`\begin{aligned}\textsf{Step 3:} \quad y-y_1&=m(x-x_1)\;\; \sf Q(6,-2)\\y-(-2)&=-4(x-6)\end{aligned}`

`\textsf{Step 4:} \quad y+2=-4x+24`

`\textsf{Step 5:} \quad y+2-2=-4x+24-2`

`\textsf{Step 6:} \quad y=-4x+22`

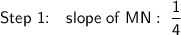
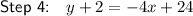
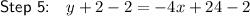
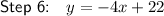
Therefore, step 2 has been completed incorrectly.

The correct answer is y = -4x + 22.