Answer:
4. no origin symmetry
Explanation:
Functions are symmetric with respect to the x-axis if for every point (a, b) on the graph, there is also a point (a, −b) on the graph:
To determine if a graph is symmetric with respect to the x-axis, replace all the y's with (−y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the x-axis.
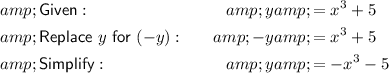
Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the x-axis.
--------------------------------------------------------------------------------------------------
Functions are symmetric with respect to the y-axis if for every point (a, b) on the graph, there is also a point (-a, b) on the graph:
To determine if a graph is symmetric with respect to the x-axis, replace all the x's with (−x). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the y-axis.

Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the y-axis.
--------------------------------------------------------------------------------------------------
Functions are symmetric with respect to the origin if for every point (a, b) on the graph, there is also a point (-a, -b) on the graph:
To determine if a graph is symmetric with respect to the origin, replace all the x's with (−x) and all the y's with (-y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the origin.

Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the origin.