Question

NO LINKS!!

Consider the following equation.
y = x^3 + 5
Test for symmetry. (select all that apply)
1. x-axis symmetry
2. y-axis symmetry
3. origin symmetry
4. no origin symmetry

Graph the equation.

Answer 1

• 4. no origin symmetry

-----------------------------

Given function:

• y = x³ + 5

Graph it first (see attached).

Test the graph for symmetry.

We know the odd degree parent function y = x³ has an origin symmetry, whilst even degree functions may have axis symmetry.

The given function is a translation of cubic function 5 units up so the center of symmetry has translated as well. Therefore correct answer is 4.

Answer 2

4. no origin symmetry

Explanation:

Functions are symmetric with respect to the x-axis if for every point (a, b) on the graph, there is also a point (a, −b) on the graph:

• f(x, y) = f(x, −y)

To determine if a graph is symmetric with respect to the x-axis, replace all the y's with (−y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the x-axis.

`\begin{aligned}&\textsf{Given}: \quad &y &= x^3 + 5\\&\textsf{Replace $y$ for $(-y)$}: \quad &-y &= x^3 + 5\\&\textsf{Simplify}: \quad &y &= -x^3 - 5\end{aligned}`

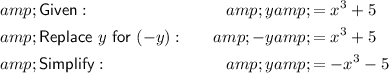
Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the x-axis.

--------------------------------------------------------------------------------------------------

Functions are symmetric with respect to the y-axis if for every point (a, b) on the graph, there is also a point (-a, b) on the graph:

• f(x, y) = f(-x, y)

To determine if a graph is symmetric with respect to the x-axis, replace all the x's with (−x). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the y-axis.

`\begin{aligned}&\textsf{Given}: \quad &y&=x^3+5\\&\textsf{Replace $x$ for $(-x)$}: \quad &y&=(-x)^3+5\\&\textsf{Simplify}: \quad &y&=-x^3+5\end{aligned}`

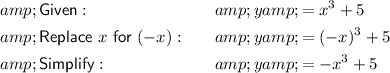
Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the y-axis.

--------------------------------------------------------------------------------------------------

Functions are symmetric with respect to the origin if for every point (a, b) on the graph, there is also a point (-a, -b) on the graph:

• f(x, y) = f(-x, -y)

To determine if a graph is symmetric with respect to the origin, replace all the x's with (−x) and all the y's with (-y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the origin.

`\begin{aligned}&\textsf{Given}: \quad &y&=x^3+5\\&\textsf{Replace $x$ for $(-x)$ and $y$ for $(-y)$}: \quad &(-y)&=(-x)^3+5\\&\textsf{Simplify}: \quad &-y&=-x^3+5\\&&y&=x^3-5\end{aligned}`

Therefore, since the resultant expression is not equivalent to the original expression, it is not symmetric with respect to the origin.