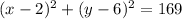Question

NO LINKS!!

Write the standard form of the equation of the circle with the given characteristics.
Center: (2, 6); Solution point: (-3, 18)

Answer 1

`(x-2)^2+(y-6)^2=169`

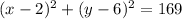
Explanation:

`\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Given:

• Center = (2, 6)
• Point on the circle = (-3, 18)

Substitute the given center and point into the equation of a circle formula and solve for r²:

`\implies (-3-2)^2+(18-6)^2=r^2`

`\implies (-5)^2+(12)^2=r^2`

`\implies 25+144=r^2`

`\implies 169=r^2`

`\implies r^2=169`

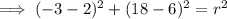
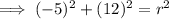
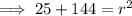
Therefore, the standard form of the equation of the circle with the given characteristics is:

`(x-2)^2+(y-6)^2=169`