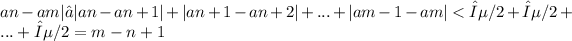Question

Give the definition of a Cauchy sequence. (i) Let (In)neN be a Cauchy sequence with a subsequence (Pm)neN satisfying limkom = 2, show that lim.In = a. (ii) Use the definition to prove that the sequence (an)neN defined by an is a Cauchy sequence.

Answer 1

`an - am| ≤ |an - an+1| + |an+1 - an+2| +...+ |am-1 - am| < ε/2 + ε/2 +...+ ε/2= m-n+1`times
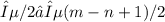`ε/2≤ ε(m-n+1)/2`, which shows that (an)neN is a Cauchy sequence.

A Cauchy sequence is a sequence whose terms become arbitrarily close together as the sequence progresses.

It is a sequence of numbers such that the difference between the terms eventually approaches zero.

In other words, for any positive real number ε, there exists a natural number N such that if m,n ≥ N then the difference between In and Im is less than ε.

(i) Let (In)neN be a Cauchy sequence with a subsequence (Pm)neN satisfying limkom = 2, show that lim.In = a.

As the sequence (In) is Cauchy, let ε > 0 be given.

Choose N such that |In - Im| < ε/2 for all m, n > N.

Since the sequence (Pm) is a subsequence of (In), there exists some natural number M such that Pm = In for some m > N.

Now, choose k > M such that |Pk - 2| < ε/2.

Then, for all n > N, we have|In - a| ≤ |In - Pk| + |Pk - 2| + |2 - a|< ε/2 + ε/2 + ε/2= ε, which shows that lim.In = a.

(ii) Use the definition to prove that the sequence (an)neN defined by an is a Cauchy sequence.

Let ε > 0 be given.

Then there exists some natural number N such that |an - am| < ε/2 for all m, n > N, since (an)neN is Cauchy.