Question

The temperature inside my refrigerator is about 40 Celsius. That temperature in Kelvin is K.

I place a balloon in my fridge that initially has a temperature of 220 C. This is K.

If the original volume of the balloon is 0.5 liters, what will be the volume of the balloon when it is fully cooled by my refrigerator? liters. (Round to two decimal places)

Answer 1

The final volume of the balloon, when completely cooled in the refrigerator, will be approximately 0.32 liters.

To solve this problem, we need to use Charles's law, which states that, at constant pressure, the volume of a sample of gas is directly proportional to its temperature.

The law can be expressed mathematically as:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{ (V_1)/(T_1)=(V_2)/(T_2) } \end{gathered}$} }`

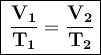
Where:

• V₁ is the initial volume
• T₁ is the initial temperature
• V₂ is the final volume
• T₂ is the final temperature

Now we obtain the data to continue solving:

• V₁ = 0.5 L
• T₁ = 220 °C
• V₂ = ?
• T₂ = 40 °C

Now, we will convert the temperatures to Kelvin:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_1=220 \ ^(\circ)C+273=493 \ Kelvin} \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_2=40 \ ^(\circ)C+273= 313 \ Kelvin} \end{gathered}$} }`

Now we solve for V₂:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=(V_1T_2)/(T_1 ) } \end{gathered}$} }`

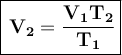
Where:

• V₁ is the initial volume
• T₁ is the initial temperature
• V₂ is the final volume
• T₂ is the final temperature

Now, we substitute the values in the formula:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=\frac{(0.5 \ L*313\\ot{k} )}{493\\ot{k} } } \end{gathered}$} }`

`\boxed{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2\approx0.32 \ Liters } \end{gathered}$} }}`

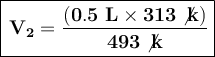
The final volume of the balloon, when completely cooled in the refrigerator, will be approximately 0.32 liters.