Question

1. For the equation of a hyperbola, identify the asymptotes:
-4x² + 40x+25y2-100y +100=0.

Answer 1

Equations of asymptotes are
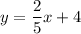`\displaystyle y=(2)/(5)x+4` and
`\displaystyle y=-(2)/(5)x`

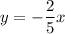
Explanation:

Determine the equation of the hyperbola by completing the square:

`-4x^2+40x+25y^2-100y+100=0\\\\-4(x^2+10x)+25(y^2-4y+4)=0\\\\-4(x^2+10x+25)+25(y-2)^2=0-4(25)\\\\-4(x+5)^2+25(y-2)^2=-100\\\\((x+5)^2)/(25)-((y-2)^2)/(4)=1`

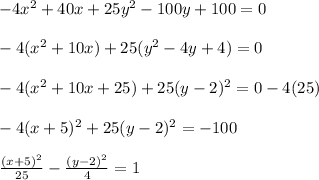
Therefore,
`a=5` and
`b=2` with center
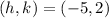`(h,k)=(-5,2)`. The asymptotes of the hyperbola can be determined with the equation
`\displaystyle y=\pm(b)/(a)(x-h)+k`:

`\displaystyle y=\pm(b)/(a)(x-h)+k\\\\y=\pm(2)/(5)(x-(-5))+2\\\\y=\pm(2)/(5)(x+5)+2`

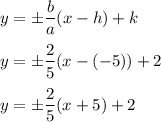
The first equation is:

`\displaystyle y=(2)/(5)(x+5)+2\\\\y=(2)/(5)x+2+2\\\\y=(2)/(5)x+4`

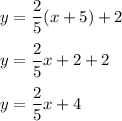
The second equation is:

`\displaystyle y=-(2)/(5)(x+5)+2\\\\y=-(2)/(5)x-2+2\\\\y=-(2)/(5)x`

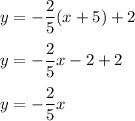
I've attached a graph to provide a visual of everything. Hopefully, it helps!