Question

The initial temperature of a balloon is 25 degrees Celsius. This is K.

How hot will a 2.3 L balloon have to get to expand to a volume of 4.6 L? K , or
Celsius..

Answer 1

The temperature that the balloon must reach to expand to a volume of 4.6 L is 596 Kelvin.

To solve this problem, we can use Charles' Law, which states that the volume of a gas is directly proportional to its temperature, as long as a constant pressure is maintained.

The mathematical formula for Charles' Law is:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{(V_1)/(T_1)=(V_2)/(T_2) } \end{gathered}$} }`

Where:

• V₁ is the initial volume
• T₁ is the initial temperature
• V₂ is the final volume
• T₂ is the final temperature

In this case, we have the following values:

• V₁ = 2.3 L
• T₁ = 25 °C + 273 = 298 K
• V₂ = 4.6 L
• T₂ = ?

We can rearrange the Charles Law formula to solve for T₂:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_2=(V_2T_1)/(V_1) } \end{gathered}$} }`

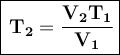
Where:

• V₁ is the initial volume
• T₁ is the initial temperature
• V₂ is the final volume
• T₂ is the final temperature

Substituting the known values:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_2=\frac{(4.6 \\ot{L}*298 \ K) }{2.3\\ot{L}} } \end{gathered}$} }`

`\boxed{\bf{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_2=596 \ Kelvin=323 \ ^(\circ)C } \end{gathered}$} }}}`

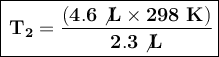
The temperature that the balloon must reach to expand to a volume of 4.6 L is 596 Kelvin.

NOTE: The temperature in degrees Celsius (°C), in these types of exercises are always converted into Kelvin (K).