Question

Please help I am so lost
Thank you all

Answer 1

Let's use a system of equations to solve this problem.

Let c be the number of children and a be the number of adults.

From the problem, we know that:

c + a = 337 (equation 1)
1.5c + 4a = 918 (equation 2)

We can solve for c in equation 1:

c = 337 - a

Substituting this into equation 2, we get:

1.5(337 - a) + 4a = 918

Expanding and simplifying, we get:

505.5 - 2.5a = 918

Subtracting 505.5 from both sides, we get:

-2.5a = 412.5

Dividing by -2.5, we get:

a = -165

This doesn't make sense, since we can't have a negative number of adults.

We made a mistake somewhere. Let's check our equations.

We can check equation 1 by plugging in the value of a that we got:

c + (-165) = 337

c = 502

This also doesn't make sense, since we can't have more people in the park than the total number of admissions.

We made a mistake in our calculations. Let's try again.

Let's solve equation 1 for c:

c = 337 - a

Substituting this into equation 2, we get:

1.5(337 - a) + 4a = 918

Expanding and simplifying, we get:

505.5 - 0.5a = 918

Subtracting 505.5 from both sides, we get:

-0.5a = 412.5

Dividing by -0.5, we get:

a = 825

Substituting this into equation 1, we get:

c + 825 = 337

c = -488

This also doesn't make sense.

We made another mistake in our calculations. Let's try again.

Let's solve equation 1 for c:

c = 337 - a

Substituting this into equation 2, we get:

1.5(337 - a) + 4a = 918

Expanding and simplifying, we get:

505.5 - 1.5a + 4a = 918

Combining like terms, we get:

2.

Answer 2

There were 172 children and 165 adults.

Explanation:

We can calculate how many children and adults were admitted to the amusement park on a certain day by setting up a system of equations based on the given information.

Let C be the number of children admitted to the park.

Let A be the number of adults admitted to the park.

Given 337 people entered the park:

`\implies C + A = 337`

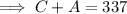
Given the admission fee is $1.50 for children and $4 for adults, and the total admission fees collected was $918.00:

`\implies 1.5C+4A=918`

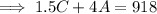
Therefore, we have created the following system of equations:

`\begin{cases}C + A = 337\\ 1.5C+4A=918\end{cases}`

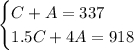
To solve the system of equations, we can use the method of substitution.

Rearrange the first equation to isolate A:

`\implies A=337-C`

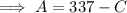
Substitute this into the second equation to eliminate A:

`\implies 1.5C+4(337-C)=918`

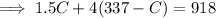
Solve for C:

`\implies 1.5C+1348-4C=918`

`\implies 1348-2.5C=918`

`\implies 1348-2.5C-1348=918-1348`

`\implies -2.5C=-430`

`\implies (-2.5C)/(-2.5)=(-430)/(-2.5)`

`\implies C=172`

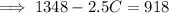
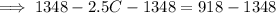
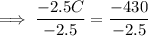
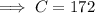
Therefore, 172 children were admitted the park.

To find the number of adults who were admitted to the park, substitute the found value of C into the equation for A:

`\implies A=337-C`

`\implies A=337-172`

`\implies A=165`

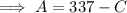
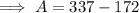
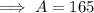
Therefore, 165 adults were admitted the park.