Answer:
Angles:
- m∠A = 51.3°
- m∠B = 38.7°
- m∠C = 90°
Sides:
- AB = 16 units
- BC = 2√(39) units ≈ 12.5 units
- AC = 10 units
Explanation:
When "solving a triangle" we need to find the measures of all three interior angles, and the lengths of all three sides of the triangle.
Angles
Since the triangle is a right triangle, we can use trigonometric ratios to find the measure of one of the unknown angles. Side AC is adjacent to angle A and side AB is the hypotenuse of the triangle, so we can use the cosine trigonometric ratio.

Given than AC = 10 and AB = 16:
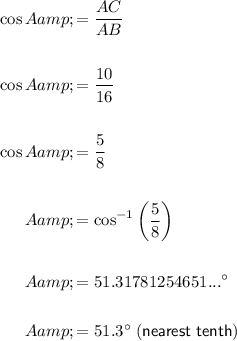
Now, use the fact that the interior angles of a triangle sum to 180° to determine the measure of angle B.
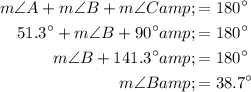
Therefore, the measures of all three angles of the right triangle are:
- m∠A = 51.3°
- m∠B = 38.7°
- m∠C = 90°
Side lengths
As the triangle is a right triangle, we can use Pythagoras Theorem to find the measure of leg BC (the leg opposite angle A).

Given AC = 10 and AB = 16, substitute these values into the formula and solve for BC:

Therefore, the lengths of all three sides of the right triangle are:
- AB = 16 units
- BC = 2√(39) units ≈ 12.5 units
- AC = 10 units