a) To find a function f such that
 , we need to find the potential function f(x, y, z) whose gradient is equal to
, we need to find the potential function f(x, y, z) whose gradient is equal to
 .
.
Given
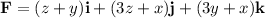 , we can find the potential function f(x, y, z) by integrating the components of
, we can find the potential function f(x, y, z) by integrating the components of
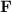 with respect to their corresponding variables:
with respect to their corresponding variables:
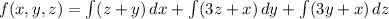
Integrating each component:

where g_1(y, z), g_2(x, z), and g_3(x, y) are arbitrary functions of their respective variables.
To satisfy the condition f(0, 0, 0) = 0, we set the arbitrary functions g_1(y, z), g_2(x, z), and g_3(x, y) to be zero:
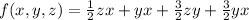
Therefore, the function f(x, y, z) that satisfies
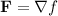 and f(0, 0, 0) = 0 is:
and f(0, 0, 0) = 0 is:
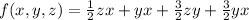
b) Now, we want to compute the line integral
 along any curve C from (0, 0, 0) to (1, 1, 1).
along any curve C from (0, 0, 0) to (1, 1, 1).
Using the fundamental theorem of line integrals, we can evaluate the line integral by evaluating the potential function f at the endpoints of the curve:

Substituting the values into the potential function:
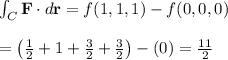
Therefore, the line integral
 along any curve C from (0, 0, 0) to (1, 1, 1) is
along any curve C from (0, 0, 0) to (1, 1, 1) is
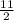 .
.