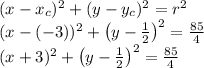Question

Find an equation of the circle who’s diameter has endpoints (-4,-4) and (-2,5)

Answer 1

`(x+3)^2+\left(y-(1)/(2)\right)^2=(85)/(4)`

Explanation:

Since the diameter of the circle has endpoints (-4,-4) and (-2,5), then the midpoint of these endpoints is the center of the circle as follows:

`(x_(c),y_(c))=\left((-4+(-2))/(2),(-4+5)/(2)\right)=\left(-3,(1)/(2)\right)\\`

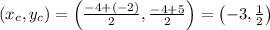
Also notice that the radius of the circle is one-half of the distance from the point (-4,-4) to the point (-2,5) as follows:

`r=(1)/(2)√((-2-(-4))^2+(5-(-4))^2)\\r=(1)/(2)√(4+81)\\r=(1)/(2)√(85)\\\\r^(2)=(85)/(4)`

Then, the equation of the circle would be:

`(x-x_(c))^2+(y-y_(c))^2=r^2\\(x-(-3))^2+\left(y-(1)/(2)\right)^2=(85)/(4)\\(x+3)^2+\left(y-(1)/(2)\right)^2=(85)/(4)`