Question

NO LINKS!! URGENT HELP!!

Calculate the AREA of the following figures.

Answer 1

A. 12 units square

B. 12 units square

C. 20 unit square

Explanation:

A. Coordinate of Traingle F(-2,-3),G(-2,3) and H(2,0)

ANS:
The distance formula is used to find the distance between two points in a coordinate plane. The formula is:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

where:

• d is the distance between the two points
• 
  `x_1` and
  `y_1`are the coordinates of the first point
• 
  `x_2` and
  `y_2`are the coordinates of the second point

Using the distance formula, we can find the lengths of the sides of the triangle.

The distance between F and G is:

a=FG=
`√((-2 - (-2))^2 + (3 - (-3))^2) = √( 36) = 6`

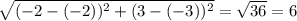
The distance between G and H is:

b=
`GH = √((2 -(- 2))^2 + (0 - 3)^2)= √(16+9)=5`

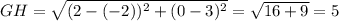
The distance between F and H is:

c=
`FH = √((2 - (-2))^2 + (0 - (-3))^2) = √(16 + 9)= √(25) = 5`

Now that we know the lengths of the sides of the triangle, we can use the formula for the area of a triangle to find the area of the triangle.

The formula for the area of a triangle is:

`A = √(s(s - a)(s - b)(s - c))`

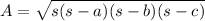
where:

• A is the area of the triangle
• s is the semi-perimeter of the triangle
• a, b, and c are the lengths of the sides of the triangle

The semi-perimeter of the triangle is:

`s = (a + b + c)/(2) = (6+5+5)/(2)=8`

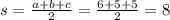
Plugging in the values for s, a, b, and c, we get:

`A=√(8(8-6)(8-5)(8-5))=12`

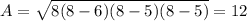
Therefore, the area of the triangle is 12 units square.

B, Coordinate of rectangle T(1,-2),U(4,1),V(2,3) and W(-1,0)

ANS:

We can find the lengths of the sides of the rectangle using the distance formula. The distance formula is:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

where:

• d is the distance between the two points
• 
  `x_1` and
  `y_1`are the coordinates of the first point
• 
  `x_2` and
  `y_2`are the coordinates of the second point

Using the distance formula, we can find the lengths of the sides of the rectangle as follows:

`UT=√((4 - 1)^2 + (1 - (-2))^2) = 3\sqrt2`

`UV = √((2 - 4)^2 + (3 - 1)^2)= 2\sqrt2`

`VW= √((-1 - 2)^2 + (0 - 3)^2) =3\sqrt2`

`WT = √((1 - (-1))^2 + ((-2) - 0)^2)= 2\sqrt2`

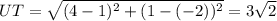
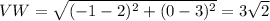
since the opposye side are equal, so it's a rectangle.

Finding the area of the rectangle:

Area = length * width

where:

• Area is the area of the rectangle
• length is the length of one of the sides of the rectangle
• width is the length of one of the sides of the rectangle

Plugging in the values for length and width, we get:

`length=3\sqrt2`

`breadth=2\sqrt2`

`Area = 3\sqrt2 * 2\sqrt2 = 12`

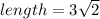
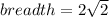
Therefore, the area of the rectangle is 12 units square.

C. Coordinate of square Q(-4,0),R(-2,4),S(2,2),T(0,-2)

ANS:

Finding the length of one of the sides:

We can find the length of one of the sides of the square using the distance formula. The distance formula is:

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

where:

d is the distance between the two points

`x_1` and
`y_1`are the coordinates of the first point

`x_2` and
`y_2`are the coordinates of the second point

Using the distance formula,

`QR= √((-2 - (-4))^2 + (4 - 0)^2) = 2\sqrt5`

`SR= √((-2 - 2)^2 + (4 - 2)^2) = 2\sqrt5`

`TS= √((0 - 2)^2 + (-2- 2)^2) = 2\sqrt5`

`QT= √((0 - (-4))^2 + (-2- 0)^2) = 2\sqrt5`

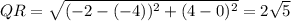
Since all the side are equal, so its a square having length
`2\sqrt5`

we have

Area of square = side²

• Area is the area of the square
• side is the length of one of the sides of the square

Plugging in the value for side, we get:

`Area = (2\sqrt5)^2 = 20`

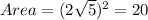
Therefore, the area of the square is 20 unit square.