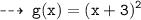Question

The graph of the function g(x) is a transformation of the parent function f(x)=x^2.

Which equation describes the function g?

​g(x)=x^2+3​

​g(x)=(x+3)^2​

g(x)=(x−3)^2

g(x)=x^2−3

Answer 1

Here we go ~

The fuction f(x) = x², as represented in the graph. we now need to fond the equation of function G(x) which is same as function f(x) but slightly displaced to the left side of x - axis.

As we know, when the displacement is along negative x - axis (let it be c), the function changes as :

`\qquad\displaystyle \tt \dashrightarrow \: g(x) = f(x + c)`

`\qquad\displaystyle \tt \dashrightarrow \: g(x) = (x + c) {}^(2)`

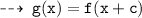
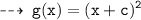
Now, lets check it out to fond the value of c ~

put value of x and y from any point on the graph of g(x)

[ let it be (-3, 0) ]

`\qquad\displaystyle \tt \dashrightarrow \: 0 =( - 3 + c) {}^(2)`

`\qquad\displaystyle \tt \dashrightarrow \: 0 = ( - 3 + {c}^{} )`

`\qquad\displaystyle \tt \dashrightarrow \: c = 0 + 3`

`\qquad\displaystyle \tt \dashrightarrow \: c = 3`

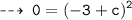
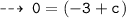
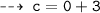
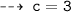
now, plug in the value of of c in the required equation and its done ~

`\qquad\displaystyle \tt \dashrightarrow \: g(x) = (x + 3) {}^(2)`