Certainly! Here are the steps to prove the trigonometric identity :
Step 1: Start with the left-hand side of the equation:
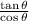
Step 2: Use the identity $$\sf\:\tan \theta = \frac{{\sin \theta}}{{\cos \theta}}\\$$ to rewrite the numerator:
$$\sf\:\frac{{\frac{{\sin \theta}}{{\cos \theta}}}}{{\cos \theta}}\\$$
Step 3: Simplify the fraction by multiplying the numerator and denominator by $$\sf\:\cos \theta\\$$:
$$\large\sf\:\frac{{\sin \theta}}{{\cos \theta}} \cdot \frac{{\cos \theta}}{{\cos \theta}}\\$$
Step 4: Cancel out the $$\sf\:\cos \theta\\$$ terms in the numerator and denominator:
$$\sf\:\sin \theta\\$$
Step 5: Rewrite the right-hand side of the equation:
$$\sf\:\frac{{\sin \theta}}{{1 - \sin^2 \theta}}\\$$
Step 6: Replace $$\sf\:\theta with \delta\\$$ to represent delta:
$$\sf\:\frac{{\sin \delta}}{{1 - \sin^2 \delta}}\\$$
Therefore, the equation $$\sf\:\frac{{\tan \theta}}{{\cos \theta}} = \frac{{\sin \theta}}{{1 - \sin^2 \theta}} {\text{can be represented as}} \frac{{\tan \delta}}{{\cos \delta}} = \frac{{\sin \delta}}{{1 - \sin^2 \delta}}\\$$ when using delta $$\sf\:(\delta)\\$$ to represent the angle.
♥️