(b) To calculate the Fourier transform of (1/3)ⁿ⁻², we'll follow a similar approach. Let's substitute the signal into the D T F T formula
X (
 ) = Σ (1/3)ⁿ⁻²
) = Σ (1/3)ⁿ⁻²
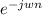
Again, let's rewrite the summation limits to simplify the calculation:
X (
 ) = Σ (1/3)ⁿ⁺¹
) = Σ (1/3)ⁿ⁺¹
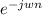
Splitting the summation into two parts
X (
 ) = (1/3)⁻¹ + Σ (1/3)ⁿ⁺¹
) = (1/3)⁻¹ + Σ (1/3)ⁿ⁺¹
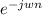
X (
 ) = 3 + Σ (1/3)ⁿ⁺¹
) = 3 + Σ (1/3)ⁿ⁺¹
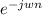
The first term in the equation represents a constant, and the second term represents a geometric series. Using the formula for the sum of a geometric series
X (
 ) = 3 + (1/3) Σ (
) = 3 + (1/3) Σ (
 )ⁿ
)ⁿ
X (
 ) = 3 + (1/3) ( 1 / (1 -
) = 3 + (1/3) ( 1 / (1 -
 ))
))
Simplifying further
X (
 ) = 3 + 1 / (3 (1 -
) = 3 + 1 / (3 (1 -
 ))
))
Therefore, the of the given signal is
X (
 ) = 3 + 1 / (3 (1 -
) = 3 + 1 / (3 (1 -
 ))
))