Answer:
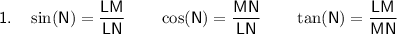

Explanation:
Trigonometric ratios are mathematical functions that relate the angles of a right triangle to the ratios of the lengths of its sides.
The three primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios are defined as follows:

Question 1
From inspection of the given diagram, we can see that the indicated angle in right triangle LMN is ∠N.
The side opposite ∠N is LM, the side adjacent ∠N is MN, and the hypotenuse of the right triangle is LN. Therefore:
Substitute these values into the trigonometric ratios:
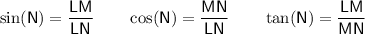

Question 2
From inspection of the given diagram, we can see that the indicated angle in right triangle LMN is ∠L.
The side opposite ∠L is MN, the side adjacent ∠L is LM, and the hypotenuse of the right triangle is LN. Therefore:
Substitute these values into the trigonometric ratios:
