Question

100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answer 1

Explanation:

A. The formula for the surface area of a hemisphere is:

SA = 2πr^2

where r is the radius of the great circle. Since we are given that the radius of the great circle is 8 yd, we can substitute this value into the formula:

SA = 2π(8 yd)^2

Simplifying, we get:

SA = 2π(64 yd^2)

SA = 128π yd^2

Therefore, the surface area of the given hemisphere is 128π square yards.

B. The formula for the surface area of a sphere is:

SA = 4πr^2

where r is the radius of the sphere. Since we are given the area of the great circle, we can use the formula for the area of a circle to find the radius:

A = πr^2

r^2 = A/π

r^2 = 28.6 in²/π

r ≈ 3.4 in

Substituting this value into the formula for the surface area of a sphere, we get:

SA = 4π(3.4 in)^2

SA ≈ 146.1 in²

Therefore, the surface area of the given sphere is approximately 146.1 square inches.

Answer 2

A. 603.19 yd²

B. 114.4 in²

Explanation:

A. The surface area of a hemisphere is equal to half the surface area of a sphere plus the area of the base of the hemisphere.

The surface area of a sphere is given by the formula A = 4πr², where r is the radius of the sphere.

The area of the base of a hemisphere is given by the formula:

A = π r². Therefore, the surface area of a hemisphere is given by the formula:

A = 2πr^2 + πr^2 = 3πr^2

In this case, the radius of the hemisphere is 8 yards, so the surface area is:

A = 3π 8²yd² = 192π yd² approx 603.19 yd²

B. The surface area of a sphere is given by the formula A = 4πr^2,

where $r$ is the radius of the sphere.

The area of a great circle is given by the formula

A = πr^2.

Therefore, the radius of the sphere is given by the formula

`r = √(A / \pi) = \sqrt{28.6 \text{ in}^2 / \pi} \approx 3.017 \text{ in}`

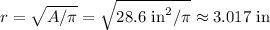
Therefore, the surface area of the sphere is A = 4π*3.017² in^2 approx 114.4in².

Another way.

Surface Area of sphere: 4*area of great square:4*28.6=114.4 in²