Question

Donnez l’intégral de -x+5/(x^2-4x+4)(x+1)

Answer 1

`(2)/(3)\ln(x+1)-(1)/(x-2) -(2)/(3)\ln(x-2)+C`

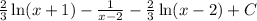
Explanation:

Integrate the following expression.

`\int (-x+5)/((x^2-4x+4)(x+1))`

`\hrulefill`

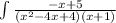
In order to integrate this function we are gonna have to use partial fraction decomposition. Start by factoring the the denominator completely.

`\int (-x+5)/((x^2-4x+4)(x+1))dx\\\\\Longrightarrow \int (-x+5)/((x-2)^2(x+1))dx`

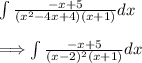
Now we can apply partial fractions. Partial fractions allows us to split up complex fractions, in doing so this will make them easier to integrate.

`(-x+5)/((x-2)^2(x+1))=(A)/(x+1)+(B)/((x-2)^2)+(C)/(x-2)\\\\\Longrightarrow (-x+5)/((x-2)^2(x+1))=(A)/(x+1)+(B)/((x-2)^2)+(C)/(x-2) \Big](x-2)^2(x+1)\\\\\Longrightarrow \boxed{-x+5=A(x-2)^2+B(x+1)+C(x-2)(x+1)}`

Expand the right-hand-side and use the comparison method to find the values of the undetermined coefficients, A, B, and C.

`-x+5=A(x-2)^2+B(x+1)+C(x-2)(x+1)\\\\\Longrightarrow -x+5=Ax^2-4Ax+4A+Bx+B+Cx^2-Cx-2C\\\\\Longrightarrow \boxed{0x^2-x+5(1)=(A+C)x^2+(-4A+B-C)x+(4A+B-2C)(1)}`

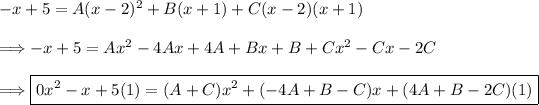
We can now form a system of equations.

For x^2 terms:

`A+C=0`

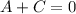
For x terms:

`-4A+B-C=-1`

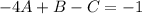
For #'s:

`4A+B-2C=5`

`\Longrightarrow \left\{\begin{array}{ccc}A+C=0\\-4A+B-C=-1\\4A+B-2C=5\end{array}\right`

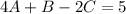
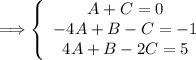
You can use any method of choice to solve the system of equations. I am going to put the system in a matrix and use my calculator to row reduce.

`\Longrightarrow \left[\begin{array}{ccc}1&0&1\\-4&1&-1\\4&1&-2\end{array}\right] =\left[\begin{array}{c}0\\-1\\5\end{array}\right]\\\\ \\ \ \ \ \Longrightarrow \left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right] =\left[\begin{array}{c}(2)/(3) \\1\\-(2)/(3)\end{array}\right]\\\\\\\therefore \boxed{A=(2)/(3), \ B=1, \ \text{and} \ C=-(2)/(3)}`

Now we can split up the fraction.

`(-x+5)/((x-2)^2(x+1))=(A)/(x+1)+(B)/((x-2)^2)+(C)/(x-2)\\\\\Longrightarrow \boxed{(-x+5)/((x-2)^2(x+1))=((2)/(3) )/(x+1)+(1)/((x-2)^2)+(-(2)/(3))/(x-2)}`

We can integrate the three fractions separately.

`\Longrightarrow \int ((2)/(3) )/(x+1)dx+ \int (1)/((x-2)^2)dx+\int (-(2)/(3))/(x-2)dx\\\\\Longrightarrow \boxed{(2)/(3)\int (1 )/(x+1)dx+ \int (1)/((x-2)^2)dx-(2)/(3)\int (1)/(x-2)dx}\\\\`

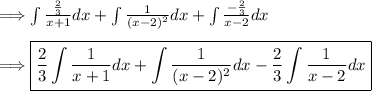
For the first integral let u=x+1 => du=dx, for the second let v=x-2 => dv=dx, and for the third integral let w=x-2 => dw=dx

`\Longrightarrow (2)/(3) \int (1 )/(u)du+ \int (1)/(v^2)dv-(2)/(3)\int (1)/(w)dw\\\\\Longrightarrow \boxed{(2)/(3) \int (1 )/(u)du+ \int v^(-2)dv-(2)/(3)\int (1)/(w)dw}`

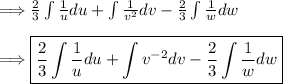
Use the rules of integration to integrate.

`\boxed{\left\begin{array}{ccc}\text{\underline{Natural Log Rule:}}\\\\ \int(1)/(x)dx=\ln(x) \end{array}\right} \ \ \boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\ \int x^ndx=(x^(n+1))/(n+1) \end{array}\right}`

`(2)/(3) \int (1 )/(u)du+ \int v^(-2)dv-(2)/(3)\int (1)/(w)dw\\\\\Longrightarrow (2)/(3)\ln(u)-v^(-1)-(2)/(3)\ln(w)+C\\\\\Longrightarrow (2)/(3)\ln(x+1)-(x-2)^(-1)-(2)/(3)\ln(x-2)+C\\\\\Longrightarrow (2)/(3)\ln(x+1)-(1)/(x-2) -(2)/(3)\ln(x-2)+C\\\\\therefore \boxed{\boxed{\int (-x+5)/((x^2-4x+4)(x+1))=(2)/(3)\ln(x+1)-(1)/(x-2) -(2)/(3)\ln(x-2)+C}}`

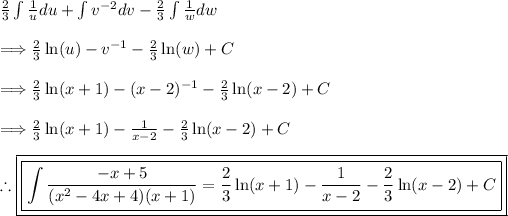
Thus, the given integral is solved where "C" is some arbitrary constant that can be found given an initial condition.