Answer:
B. 8 inches
Explanation:
The question tells us that a cylinder and a cone have the same volumes, and also tells us the height and radius of the cylinder, as well as the radius of the cone. The question then asks us to calculate the height of the cone.
In order to solve the problem, let's first calculate the volume of the cylinder using the formula:
 ,
,
where:
V = volume of cylinder
r = radius of cylinder (8 in.)
h = height of cylinder (6 in.)
Therefore,
volume of cylinder =
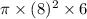
=
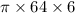
=
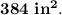
The volume of a cone is given by the formula:
 ,
,
where:
V = volume of cone (384π in³)
r = radius of cone (12 in.)
h = height of cone
Given that the volumes of the cone and the cylinder are equal, the cone's volume is also 384π in³. Hence, we can solve for the value of h:
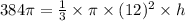
⇒

⇒
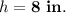
Therefore, the height of the given cone is 8 inches, and the correct option is B.