Question

A quadratic equation, y = ax^2 - 6x + 10, has exactly one real root. Calculate the value of a.

Answer 1

a = 0.9

Explanation:

For the quadratic equation
`\boxed{ax^2 + bx + c = 0}` to have exactly one real root, the value of its discriminant,
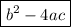`\boxed{b^2 - 4ac}`, must be zero.

For the given equation:

`y = ax^2 - 6x + 10`,

• a = a

• b = -6

• c = 10.

Substituting these values into the formula for discriminant, we get:

`(-6)^2 - 4(a)(10) = 0`

⇒
`36 - 40a = 0`

⇒
`36 = 40a`

⇒
`a = (36)/(40)`

⇒
`a = \bf 0.9`

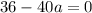
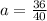
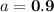
Therefore the value of a is 0.9 when the given quadratic has exactly one root.