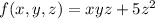Question

Consider F and C below. F(x, y, z) = y2 i + xz j + (xy + 18z) k C is the line segment from (1, 0, -3) to (4, 4, 3) (a) Find a function f such that F = Vf. = f(x, y, z) = (b) Use part (a) to evaluate b

Answer 1

To find the function f such that F = Vf, we need to find the vector gradient of F and then integrate the resulting vector. The function f(x, y, z) = xy^2 + x^2z + 9xz^2 + C satisfies the given conditions. Evaluating f for the line segment C from (1, 0, -3) to (4, 4, 3) gives f(x, y, z) = xy^2 + x^2z + 9xz^2 + 244.

Step-by-step explanation:

To find a function f such that F = Vf, we need to find the vector gradient of F and then integrate the resulting vector. The vector gradient of F is given by Vf = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k. Comparing the components of F and Vf, we can conclude that ∂f/∂x = y^2, ∂f/∂y = xz, and ∂f/∂z = xy + 18z. Taking the antiderivatives, we find that f(x, y, z) = xy^2 + x^2z + 9xz^2 + C, where C is the constant of integration.

To evaluate f for the line segment C from (1, 0, -3) to (4, 4, 3), we substitute the endpoints into f. So, f(1, 0, -3) is equal to 1*0^2 + 1*1*(-3) + 9*1*(-3)^2 + C = -8 + C. Similarly, f(4, 4, 3) is equal to 4*4^2 + 4*4*3 + 9*4*3^2 + C = 244 + C. Therefore, the function f for the line segment C is f(x, y, z) = xy^2 + x^2z + 9xz^2 + 244.

Answer 2

`\(f(x,y,z)=xyz + 5z^2\)` and
`\( \int_(C) \\abla f \cdot d r \)=112`

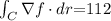
The components of the vector field
`\( \mathbf{F} \) are \( F_x = yz \), \( F_y = xz \), and \( F_z = xy + 10z \).`

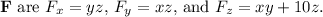
The integral of Fₓ with respect to x is
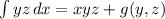`\( \int yz \, dx = xyz + g(y,z) \)`, where g(y,z) is an arbitrary function of y and z since the partial integration with respect to x does not affect y and z.

The integral of
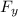`\( F_y \)` with respect to y is
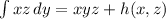`\( \int xz \, dy = xyz + h(x,z) \)`, where h(x,z) is an arbitrary function of x and z. Comparing this with the previous result, we see that g(y,z) must be a function of z only, since the term xyz is already present.

The integral of
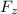`\( F_z \)` with respect to z is
`\( \int (xy + 10z) \, dz = xyz + 5z^2 + k(x,y) \)`, where k(x,y) is an arbitrary function of x and y. Since we already have xyz from the previous integrations and g(y,z) must be a function of z only, we can determine that
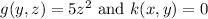`\( g(y,z) = 5z^2 \) and \( k(x,y) = 0 \)`. Therefore, the complete function f(x,y,z) is
`\(f(x,y,z)=xyz + 5z^2\)`.

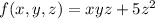The fundamental theorem of line integrals states that if f is a differentiable function of three variables whose gradient vector
`\( \\abla f \)` is continuous on a smooth curve C from point A to point B, then
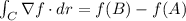`\( \int_(C) \\abla f \cdot d r = f(B) - f(A) \)`. This means we can evaluate the line integral by simply computing the difference f at the endpoints of the curve C.

The value of f at the starting point (2,0,-1) is f(2,0,-1) = (2)(0)(-1) + 5(-1)² = 5. The value of f at the ending point (6,4,3) is f(6,4,3) = (6)(4)(3) + 5(3)² = 72 + 45 = 117.

Using the fundamental theorem of line integrals, we have
`\( \int_(C) \\abla f \cdot d r = f(6,4,3) - f(2,0,-1) = 117 - 5 = 112 \)`.

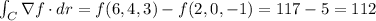Question: