Question

Find theValue of x
40°
70°
(5x+10)°

Answer 1

Hey! there . Thanks for your question :)

Answer:

• 20° is the correct answer.

Explanation:

In this question we are given with two interior angles of the triangle that are 40° and 70° , also we are given an exterior angle that is (5x + 10)°. And we are asked to find the value of angle x.

Solution :-

For finding the value of angle x , we have to use exterior angle property of triangle which states that sum of opposite interior angles of triangle is equal to the given exterior angle. So :

Step 1: Making equation :

`\longmapsto \: \sf{40 {}^(°) + 70 {}^(°) = (5x + 10) {}^(°) }`

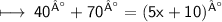
Solving :

`\longmapsto \: \sf{110 {}{°} = (5x) {}^(°) +10 {}^(°) }`

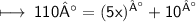
Step 2: Subtracting 10 on both sides :

`\longmapsto \sf{ 110 {}^(°) - 10 {}^(°) = 5x + \cancel{10 {}^(°)} - \cancel{10 {}^(°) } }`

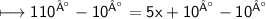
We get ,

`\longmapsto \sf{(5x ){}^(°) = 100 {}^(°) }`

Step 3: Dividing both sides by 5 :

`\longmapsto \frac{ \cancel{5}x {}^(°) }{ \cancel{5}} = \frac{ \: \: \: \: \cancel{ 100} {°}^{} }{ \cancel{5} }`

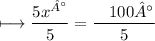
On cancelling , we get :

`\longmapsto \underline{\boxed{\red{\sf{ \bold{ x = 20 {}^(°) }}}}} \: \: \bigstar`

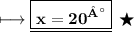
• Therefore , value of x is '20°'

Verification :-

For verifying sum of both the interior angles is equal to given exterior angles. As we get the value of x as 20 we need to substitute it's value in place x and then L.H.S must be equal to R.H.S :

• 40° + 70° = 5(20°) + 10°

• 110° = 100° + 10°

• 110° = 110°

• L.H.S = R.H.S

Therefore , our answer is correct .

• Hope , it'll help you! :)

#
`\underline{ \sf{ \bold{ Keep \: Learning }}}`

Answer 2

Here's your solution ~

Value of an exterior angle of a triangle is equal to the sum of values of two opposite interior angles of a triangle.

therefore,

`\qquad\displaystyle \tt \dashrightarrow \: 5x + 10 = 40 + 70`

`\qquad\displaystyle \tt \dashrightarrow \: 5x = 110 - 10`

`\qquad\displaystyle \tt \dashrightarrow \: 5x = 100`

`\qquad\displaystyle \tt \dashrightarrow \: x = 100 / 5`

`\qquad\displaystyle \tt \dashrightarrow \: x = 20`

Value of x = 20°