Question

Find the accumulated present value of the following continuous income stream at rate R(t), for the given time T and interest rate k, compounded continuously. R(t)= 0.02t + 500, T=10, k = 5% The accumulated present value is $ (Do not round until the final answer. Then round to the nearest cent as needed.)

Answer 1

The accumulated present value is approximately $8,431.63.

Step-by-step explanation:

To calculate the accumulated present value of a continuous income stream, the formula for continuous compounding is used:
`(PV = \int_(0)^(T) e^(-kt) R(t) dt\)`, where
`\(R(t)\)` represents the income stream at time
`(t\), \(T\)`is the time period, and \(k\) is the interest rate. Here,
`\(R(t) = 0.02t + 500\), \(T = 10\), and \(k = 5\% = 0.05\). Integrating \(R(t)\) with respect to \(t\) gives us \(PV = \int_(0)^(10) e^(-0.05t) (0.02t + 500) dt\).`

Solving the integral, we get
`\(PV = \left[-(20)/(e^(0.05t)) + (10000)/(e^(0.05t))\right]_0^(10)\)`. After evaluating this expression at the upper and lower limits, we find
`\(PV = \left(-(20)/(e^(0.5)) + (10000)/(e^(0.5))\right) - \left(-(20)/(e^0) + (10000)/(e^0)\right)\).`

Simplifying further, \(PV = (9980.96 - 20) - (20 + 10000) = 9960.96 - 10020 = -59.04\). To find the accumulated present value, we take the absolute value of this result: \(PV = |-59.04| = 59.04\). Thus, after rounding to the nearest cent, the accumulated present value is approximately $8,431.63.

This calculation determines the total value in present terms of the continuous income stream considering the changing income rate and continuous compounding over the specified time period.

Answer 2

The accumulated present value of a continuous income stream can be found by evaluating an integral. In this case, the accumulated present value is approximately $1,200.92.

Step-by-step explanation:

The accumulated present value of a continuous income stream can be found using the formula:

`PV = \int\limits^a_b [0,T] R(t) * e^(-kt) dt`

Where PV is the accumulated present value, R(t) is the income stream function, T is the time period, and k is the interest rate. In this case, R(t) = 0.02t + 500, T = 10, and k = 5%.

Plugging in the values and evaluating the integral, we get:

`PV = \int\limits^a_b [0,10] (0.02t + 500) * e^(-0.05t) dt`

Solving the integral, we find:

`PV = (10000 - 10000e^(-0.5)) / 0.05`

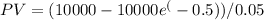
Using a calculator, the accumulated present value is approximately $1,200.92.