Question

Solve by the graphing method.

x - 2y = 9
3x - y = 7

Answer 1

Hello there ~

For graphing method, we need atleast two points lying on both the lines.

so, lets start with this one :

`\qquad\displaystyle \tt \dashrightarrow \: x - 2y = 9`

1.) put y = 0

`\qquad\displaystyle \tt \dashrightarrow \: x - 2(0) = 9`

`\qquad\displaystyle \tt \dashrightarrow \: x = 9`

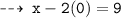
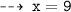
so our first point on line " x - 2y = 9 " is (9 , 0)

similarly,

2.) put x = 1

`\qquad\displaystyle \tt \dashrightarrow \: 1 - 2y = 9`

`\qquad\displaystyle \tt \dashrightarrow \: - 2y = 9 - 1`

`\qquad\displaystyle \tt \dashrightarrow \: - 2y = 8`

`\qquad\displaystyle \tt \dashrightarrow \: y = 8 / ( - 2)`

`\qquad\displaystyle \tt \dashrightarrow \: y = - 4`

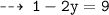
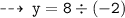
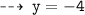
next point : (1 , -4)

Now, for the next line " 3x - y = 7 "

1.) put x = 0

`\qquad\displaystyle \tt \dashrightarrow \: 3(0) - y = 7`

`\qquad\displaystyle \tt \dashrightarrow \: - y = 7`

`\qquad\displaystyle \tt \dashrightarrow \: y = - 7`

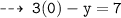
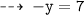
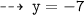
First point is (0 , -7)

2.) put x = 1

`\qquad\displaystyle \tt \dashrightarrow \: 3(1) - y = 7`

`\qquad\displaystyle \tt \dashrightarrow \: 3 - y = 7`

`\qquad\displaystyle \tt \dashrightarrow \: - y = 7 - 3`

`\qquad\displaystyle \tt \dashrightarrow \: y = - (7 - 3)`

`\qquad\displaystyle \tt \dashrightarrow \: y = - 4`

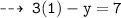
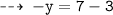
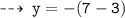
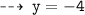
second point : (1 , -4)

Now, plot the points respectively and join the required points to draw those two lines. and the point where these two lines intersects is the unique solution of the two equations.

Check out the attachment for graph ~

Henceforth we conclude that our solution is

(1 , -4), can also be written as : x = 1 & y = -4